I Hacked an ECG Machine

Abstract

This project explores a method to extract and decode high-quality ECG data from the KardiaMobile device without relying on proprietary APIs. By leveraging the original device’s frequency-modulated (FM) audio output, I developed a pipeline for demodulating, calibrating, and denoising the signal using quadrature demodulation and adaptive filtering techniques. The approach successfully removes noise, including mains hum and harmonics, and reconstructs the ECG signal with high fidelity. This method successfully produced high-quality ECG signals, clearly showing key features such as the P-waves, the QRS-complex, and T-waves. This accessible and cost-effective solution enables incidental ECG data collection for research purposes, using the KardiaMobile’s affordable hardware.

Introduction

I’ve been interested in electrocardiograms (ECG or EKG) for several years. Back in 2017, I attempted to build my own ECG machine. While the project didn’t progress very far (resulting in a few damaged operational amplifiers), it sparked a lasting fascination with ECG technology.

This interest resurfaced when I discovered the KardiaMobile ECG devices. These pocket-sized, battery-powered machines connect to a smartphone and enable basic ECG recordings. They are approved by both the British National Institute for Health and Care Excellence (NICE) and the U.S. Food and Drug Administration (FDA). The KardiaMobile 6L even records three channels, allowing for six-lead ECGs to be synthesized. This elegant, pre-packaged solution immediately reminded me of my earlier ECG project—only someone else had done all the hard work.

The KardiaMobile is a compact device, approximately 80 mm long and 30 mm wide, with two metal electrodes for recording ECGs. It outputs the ECG signal which is then picked up by the smartphone app that seems to work on almost any phone with recordings limited to 5 minutes by the Kardia app. To record an ECG you start up the app and set it to record an ECG then place your left index finger on the left electrode and your right index finger on the right electrode. The app then detects that an ECG is now being generated and starts recording it, plotting it live on the screen. After the ECG has been acquired you can then save the ECG in the app along with tags and notes and you can also generate PDF reports that plot the ECG on a page along with basic information.

The app can even detect a few heart conditions – although it’s no substitute for a cardiologist.

While KardiaMobile devices work seamlessly with the official Kardia app to generate ECG plots and reports, my interest lay elsewhere: I wanted access to the raw ECG data to create custom visualizations and analyses. My goal wasn’t related to health monitoring or diagnosis; I simply wanted to explore the data and create neat charts.

The Problem: How to access the data?

The KardiaMobile 6L transmits ECG data to a smartphone via Bluetooth, a secure two-way protocol with encryption and numerous parameters. Extracting raw data directly seemed like a dead end. I briefly considered tracing ECG plots from the app’s reports, but having tried similar methods before, I knew how error-prone they could be. Kardia does offer an API, but it appears to be intended for clinical use, not individual hobbyists—they never responded to my inquiries.

Chance solution: The older version uses sound waves to transmit the data

By chance, I watched a cardiologist’s review of the KardiaMobile on YouTube. He mentioned that the device uses sound waves to communicate with the app. While this seemed preposterous, I decided to investigate. To my surprise, I discovered that the original KardiaMobile (single-lead) indeed transmits its signal using a frequency-modulated (FM) sound wave in the 18–20 kHz range, as specified in its documentation. The key details include:

A carrier frequency of 19 kHz
Frequency modulation with a scale of 200 Hz/mV
A 10 mV peak-to-peak range
A frequency response from 0.1 Hz to 40 Hz

Armed with this information, I mocked up a test: I generated a synthetic heartbeat, frequency-modulated it, and played it through my computer. To my amazement, the Kardia app detected it as a healthy heartbeat with a BPM of 75—precisely what I had set. Confident in my understanding of the encoding process, I purchased a KardiaMobile device to explore further.

I actually found out all of this information before purchasing an ECG machine. So I mocked up an example heartbeat, frequency modulated it and played it on my computer. The Kardia app detected it as a healthy heartbeat with a BPM of 75, exactly what I had set it as. At this point, I was pretty sure that I understood the encoding process since I had effectively reverse-engineered the protocol and had a successful test on the Kardia app. The output is one-way, analogue, and not encrypted. With this newfound confidence in my plan, I bought a KardiaMobile ECG.

Optimising the signal acquisition

While initially concerned about microphone selection, I found that the microphones on my Samsung Galaxy S20 Ultra worked well—FM modulation is forgiving. I also experimented with beamforming algorithms to improve signal-to-noise ratio (SNR), but they failed due to the directional nature of the high-frequency signal. A simpler method, selecting the channel with the most power in the carrier band, proved effective. This shouldn’t have been surprising as the app also works by using the built-in microphone on my phone, however initially I wasn’t sure how much signal processing they were doing so I wanted to get the best initial signal.

Amount of signal in carrier band received by each microphone on my phone

After I did a quick experiment where I held the Kardiamobile near my phone in different places I was able to work out where the best place to hold it was. I ended up using the bottom of the phone for all of my tests as it yielded high signal and was convenient.

Decoding the ECG Signal

The decoding process follows these steps:

Input and Preprocessing:
- Read the audio file and determine its sample rate.
- If the signal has multiple channels, select the one with the highest power in the carrier band.
FM Demodulation:
- I tested several demodulation methods, with quadrature demodulation yielding acceptable results with a simple algorithm. This calculates the frequency deviation from the carrier frequency.
Calibration and Downsampling:
- Convert the frequency deviations to voltage using the scale of 200 Hz/mV.
- Downsample the signal to 600 samples/second, as the 19 kHz carrier signal has been removed so high temporal resolution isn’t needed.
Denoising and Filtering:
- Identify and filter out mains hum (e.g., 50 Hz in the UK, including harmonics). I implemented an adaptive Fourier-based filter to detect and remove the specific mains frequency and its harmonics.
- Remove low-frequency noise (<0.52 Hz) and high-frequency noise (>40 Hz) using a zero-phase filter to avoid adding in phase distortion to the signal.
Post-Processing:
- Apply wavelet denoising using DB4 wavelets to remove noise without reducing the sharp features in the signal.
- Trim extraneous noise at the start and end of the recording.

Removing mains hum

The main source of noise was mains hum picked up by the Kardia ECG itself. An example of the filtering process is shown below, where the sharp peak near 50 Hz. I used an adaptive filtering approach that ensures precise removal even when the mains frequency slightly deviates (e.g., 49.92 Hz instead of 50 Hz) removing the minimum additional signal.

Detected Mains Frequency: 49.92 Hz
Filtering 49.92 Hz: Range [49.42, 50.42]
Filtering 99.84 Hz: Range [98.85, 100.84]
Filtering 149.77 Hz: Range [148.27, 151.26]
Filtering 199.69 Hz: Range [197.69, 201.69]
Filtering 249.61 Hz: Range [247.11, 252.11]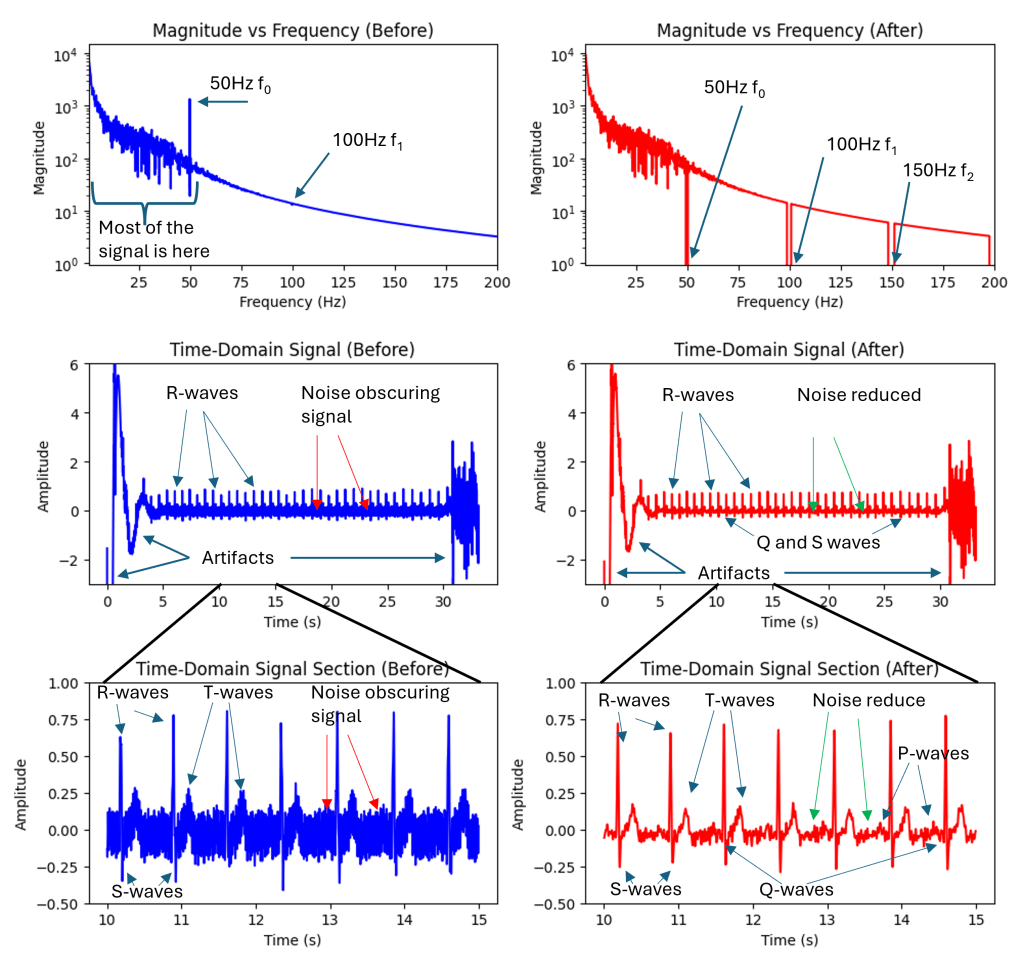

Effect of filtering out mains hum in the frequency domain and the time domain. The bottom plots are zoomed-in sections.

Since the mains frequency component is so strong the filtering process also needs to be very strong. A second-order filter with a cut-off frequency of 40Hz still left a large amount of 50Hz noise in the signal. Interestingly this 50Hz hum is not hum picked up by the microphone it’s actually hum picked up inside the Kardia unit. I used second-order zero-phase filters that avoid adding phase artifacts to the signal. Traditional filters like Butterworth filters add a phase shift that varies by frequency which can be particularly harmful to these kinds of signals.

Following this additional denoising was applied using wavelet transforms and Daubechies 4 (DB4) wavelets. This transforms the time domain signal into a signal that is made up of short bursts of short packets of waves. These efficiently model bursty signals like heartbeats and poorly model totally random signals like noise. In the wavelet domain, you can filter out small wavelet coefficients that are more likely to correspond to noise and keep coefficients of greater magnitude that are more likely to correspond to my heartbeat signal.

I then added some basic signal processing was used to estimate where the real signal started and finished (i.e., to remove the initial and final bits of noise from when Kardia unit was off).

Results

After all of these steps, I was able to produce high-quality ECG results that can be exported in any output format (.csv, .xls, .npy, .mat etc) and plotted in any way desired. Kardia likely adds lots of useful signal processing that I’m not able to reproduce at this time however I was able to produce ECG results that clearly show the main features of the expected heartbeat signal including R-waves, T-waves, S-waves, and the QRS complex.

Full signal after decoding and denoising

Signal section showing: P, QRS, and T waves

Conclusion

The result of all this is a high-quality method of recording and exporting ECG data from the Kardiamobile device without using their API which is not available to the general public. Since the Kardia device is very inexpensive – I paid around £50 (60USD or 60EURO) for mine – and this method is easy to reproduce this may open up new avenues for incidental ECG usage in a research setting. This may enable researchers to extract ECG signals from inexpensive hardware, facilitating incidental ECG usage in various research settings.

This method is obviously not appropriate for monitoring or diagnosing any kind of health condition.

An extremely rough version of this code is available at my github: https://github.com/joshuamcateer/kardiadecode

Zeiss Tessar: How does my vintage lens blur images?

Computer Vision, Optics, Photography, Projects

Modern camera lenses are typically super sharp but can sometimes lack character. Vintage lenses with fewer corrective elements are typically softer and have decreasing contrast and resolution in the corners. But what’s going on in my lens?

In this post, I’ll use computer vision techniques to analyse the performance of this vintage lens and then see what effect this has on photographs.

Lens adapted onto modern mirrorless camera

Background

The lens was a budget product from one of the premier optical manufacturers in the world, Zeiss. Zeiss has long been synonymous with excellent optics, developing many key technologies in its history. Currently, Zeiss produces extremely high-performance optics for a range of applications, including photography and photolithography – the silicon chips in your laptop and iPhone were likely manufactured using Zeiss-made photolithography systems. After the partition of Germany, Zeiss – a high-tech company critical to modern economies and militaries – was also partitioned. Much of the stock, equipment, intellectual property, and staff were taken by the Soviet Union to kick-start its optics industry and the remaining Zeiss company was split into Zeiss Oberkochen in West Germany that largely sold to the West, and Carl Zeiss Jena in East Germany that largely sold to the Soviet Union.

This lens was manufactured in 1967 by Carl Zeiss Jena and is a Zeiss Tessar design. The original Tessar was patented in 1902 which I have previously discussed, but this one was redesigned for smaller formats using the latest glasses and design techniques. It was sometimes called the eagle eye because of its centre sharpness and contrast. This is a 4 element/3 group design that performed well, especially when coating technology was in its infancy when it was important to minimise the number of glass-air interfaces to reduce flaring. This example is single-coated, has a minimum focus distance of 0.35m, uses unit focusing (the whole optical unit moves back and forth to focus), and was designed for use with 135 (35mm) film probably for colour and black and white – which were both available when this lens was manufactured. Films available in 1967 were very different to the ones available now and in the ’90s. They were slower and had more grain, Kodachrome II (I believe the most common colour film available in 1967) was available in ASA 25 and Kodachrome-X had just been released in 1962 with a speed of ASA 64. ASA speed is basically the same as ISO speed – in fact, ASA and ISO are just standard agencies (American Standards Agency and ISO kind of means International Standards Organisation, although it now isn’t an acronym and is just ISO, the Greek prefix for same) which specify how the film speed should be measured, there are ISO standards for bolts, paper sizes, and almost anything else you can think of (including how to make a cup of tea).

The lens has a five-bladed aperture, aperture clicks from f/2.8-f/22 with half stops. It has a depth of field scale, infrared focus mark, and an automatic aperture system – meaning that, on a compatible SLR, the aperture remains open for focusing and then stops down the specified setting when the shutter is depressed. It uses the M42 mount which is easily adapted to other systems due to its long back focal distance. The lens body is made of aluminium and has an attractive brushed/striped design that offers excellent grip. This particular lens had a stuck focusing helicoid, so I removed the old grease using lighter fluid, lint-free paper, and cotton buds and re-greased it with modern molybdenum grease (Liqui Moly LM47).

I wrote some software (this actually took ages) and printed off some test charts to work out exactly what my vintage Zeiss Tessar 50mm 2.8 lens is doing to my images.

Analysing the Blurring

I photographed the test charts at a set distance (0.6m) wide open (f/2.8) and stopped down (f/8). The camera was set on a stable tripod and carefully aligned so that it was perpendicular to the floor where the test chart was placed a 10-second shutter delay was used to reduce camera shake and the camera was set at its base sensitivity to minimise noise.

The software that I wrote found each of the test targets in the stopped-down image and found the corresponding test targets in the wide-open image, this is shown in Figure 0. I then assumed that the stopped-down image was perfect and used it as a reference to compare the wide-open image.

Figure 0. Computer vision algorithm automatically finds the targets in the test chart.

Using some fancy maths (called a Fourier transform) you can work out how to transform between the sharp stopped-down image and the blurred wide-open image. I did this for each target on my test chart because the amount and nature of the blurring are different across the frame.

Fig 1. Reference test chart taken at f/8 with centre and edge targets marked. The edge targets are less sharp than the centre even in the reference image.

Fig 2. Wide open test chart taken at f/2.8 with centre and edge targets marked

The above images are the photographs of the test charts photographed at the sharp aperture (f/8) and the blurred aperture (f/2.8). This method of using the sharpest aperture of the lens as the reference was used because it allows for perfect alignment of the images – both images have the same geometric distortion. A limitation of this method can be seen in Figure 1 in which the corners of the image are not perfectly sharp even at f/8. I was inspired to use this method after reading the excellent paper High-Quality Computational Imaging Through Simple Lenses by Heide et al, 2013, although the actual method that I used was different.

Fig 3. Comparison of reference and wide open targets. The central targets are slightly blurred and the edge targets are very blurred.

Enlarged examples of the test target pairs are shown in Figure 3. I then worked out exactly what blurring function you need to apply to the sharp image to produce the blurred image for each pair of targets. The result of this is shown in Figure 4, which is an array of point spread functions (PSFs). These PSFs show how each point in the image is blurred by the lens – the PSFs in Figure 4 are zoomed in 7x. Figure 4 also includes a second array of targets that is offset from the one shown in Figures 1 and 2, that’s why the PSFs are arranged in two grid patterns. The results from the two test charts agree.

Figure 4. Point spread functions at different locations over the frame. Zoomed in 7x

Figure 5. PSF from the centre of the frame. The PSF is compact with a halo around it that is mostly symmetrical. Left is the original and the right panel has increased contrast.

Figure 6. PSF from the centre of the frame. The PSF has a core and a surrounding extended diagonal line. Left is the original and the right panel has increased contrast.

Figures 5 and 6 show enlarged PSFs from Figure 4. The nature of the PSF changes over the image. The PSFs in the centre are more compact and have a distinct halo around the central region, an ideal PSF would have a central point and no surrounding detail. The halo around the points is spherical aberration, this is an optical aberration caused when rays parallel to the optical axis of the lens are focused at different distances from the lens depending on the distance from the optical axis. This causes a glowing effect in the image, since a sharp image is formed (the sharp central core of the PSF) and a blurred image of the same object is also formed but superimposed on the sharp image. This would not greatly reduce resolution but would reduce contrast. Spherical aberration should be constant over the image frame, but varies a lot with the aperture size used in the lens, stopping the lens down reduces spherical aberration quickly.

The PSF in Figure 6 mostly shows sagittal astigmatism. Astigmatism is when rays in two perpendicular planes have different focal points. Two kinds of astigmatism that occur in systems like this are tangential astigmatism and sagittal astigmatism. Tangential astigmatism points towards the optical centre of the frame and sagittal astigmatism points perpendicular to the centre of the frame. Sagittal astigmatism can cause a swirly effect in images as it blurs points into circular arcs around the optical centre. A lens with sagittal astigmatism can be refocused to give tangential astigmatism so the orientation of the astigmatism will flip around. This is because the best sagittal focus and the best tangential focus occur in different planes. Astigmatism doesn’t occur in the centre of the frame and increases rapidly towards the edge of the frame and with increasing aperture size. This aberration is sometimes called coma which is a similar but distinct aberration that looks a bit like a comet with a sharp point pointing towards the centre of the image and a fatter tail pointing away.

Above are maps of the Strehl ratio of the PSF. Strehl ratio is a simple measure of PSF quality, where higher values (maximum 1) indicate that the PSF is most similar to an ideal PSF e.g., a single point in this case. The bright greens are the regions of highest sharpness and the dark blues are the regions of lower sharpness. There is likely some noise in this estimate – I don’t completely trust it. However, from this analysis, it seems that the lens is somewhat decentred, as the sharpest region of the lens is not in the direct centre. This could be due to manufacturing defects such as the lens elements not being correctly seated, or due to damage that occurred during the previous 57 years, or due to an alignment issue with the lens adapter or the target was photographed.

An interesting feature of this lens is the apparent lack of axial chromatic aberration. The PSFs are very similar in each colour channel and the Strehl maps are also very similar, these tests are not very demanding and are not able to test at all for transverse chromatic aberration. For a lens likely designed with black and white photography in mind this is a pleasant supprise.

Example Images

Below are sample images taken with the lens at various apertures, mostly f2.8 (wide-open) and f/8. The second gallery includes zoomed-in regions to show the character of the lens in more detail. Simple colour and exposure correction was applied in Adobe Lightroom, no texture, clarity, or dehazing was added. Images were resized to 1600px on the long edge with sharpening for screen added at export.

A selected sample of images with zoomed-in regions. The image with daisies shows much greater sharpness in the centre of the image compared with the edge and some swirling effect caused by the astigmatism in the lens. The pair of images of the graffiti rabbit (f/2.8 and f/8) show the increase in contrast and sharpness as the lens is stopped down. All areas of the image show an improvement in sharpness and contrast, but the edges improve more. This is also shown in the pair of leaf images, however, the increase in depth of field in these images makes it harder to determine sharpness changes in the plane of focus. The train track images show the same trend with a distinct increase in contrast in the centre of the image (the clocktower).

The bokeh image is of running water in a canal and was taken with the lens set to close focus at f/2.8. The bokeh is bubbly with distinct outer highlights which indicates over-corrected spherical aberration, sometimes this is considered attractive such as in the Meyer Optik Goerlitz Trioplan lens, however, the effect is less strong in this Tessar. This also leads to the distracting out-of-focus elements in the last image of the dog (my beagle, Saturn) where a line out of the plane of focus is blurred into a sharply defined feature.

None of these images show chromatic aberration, this would likely be apparent on the image of the tram powerlines.

f/2.8 red lines showing the direction of the blurring causing the slight swirl effect.

Conclusion

Despite the lens being 57 years old it is still capable of producing sharp images. The lens is sharper in the centre of the frame than at the edge and the edge has a small amount of swirl effect. The lens doesn’t offer much ‘character’, which is likely expected as it was a standard lens for decades and most people want low-cost, small, sharp-enough lenses that don’t detract from the subjects being photographed. There some pleasant aspects of the lens, such as the slightly soft look that may be pleasing for some portrait work, and the bubbly bokeh may be desirable for some creative effects.

To get the most character from this lens, have a bit of separation between the subject and the background and foreground elements. Strong highlights may have a distracting or exciting bubbly effect, so stay cognisant of this. The lens has a great minimum focusing distance and so can produce quite a lot of out-of-focus blurring, it’s also a bit softer up close, so use this when you want to knock out very sharp details, such as skin texture in portraits. The lens has little chromatic aberration so don’t worry too much about that. The vibes of the lens tie the image together nicely, although they make it a little flat before contrast is added back in editing.

DIY wall-reflecting surround sound speakers

Audio, Projects

Surround sound is cool. Hearing sound effects and music coming from every angle is much more immersive than just having the sound come from your TV. However, it isn’t easy to fit so many speakers in to every type of room. People who are into hi-fi will tell you that you need to have your speakers a specific distance from the wall, and rotate them at a specific angle to get the best sonic experience in the seating position. And god forbid if you tell them that you have your sofa against the back wall… “The rear wall will enhance the bass at random frequencies, it will sound boomy and horrible”.

What do you do then, if your room isn’t the right size and shape for an ideal home cinema? What if you only have space to put a speaker on one side of the seats? Well, one thing you probably shouldn’t do is build the speakers yourself (but maybe you still should).

The room problem. A small side table on one side and the doorway on the other. No room for a speaker on the right hand side.

I wanted to install a 5.1 surround sound system, starting with a 3.0 system. If you didn’t know, the first number is the number of ‘surround speaker’, and the second number is the number of subwoofers. Typically in cinemas sounds bellow around 80Hz are played by subwoofers, and higher frequencies are played by the other speakers. 3.1 systems have a left and right speaker, and a centre channel as well as a subwoofer (the 0.1). 5.1 systems add two surround speakers what are approximately in line with the seats. 7.1 systems have another two speakers behind the seats and point towards the TV. In 2014 a new standard was created, Dolby Atmos, that adds hight channels to the sound on films. The best way to do this is to cut holes in the ceiling and place speakers pointing at the seats from the ceiling at specific locations. However, for people who can’t do this, there is also an option to have speakers pointed at the ceiling (typically on top of other speakers at ear level) and to bounce the sound off of them to the seats.

Klipsch tower speaker with ceiling-firing speaker built into the top of it.

This is all very interesting, and probably sounds great. However, I didn’t want to cut holes in the ceiling, or to buy a new receiver that can decode Dolby Atmos, and I still couldn’t fit in even a 5.0 system. I then had the idea of using the surface bouncing idea to reflect the sound off of a wall and back to the seats so that the speaker near the door would have room.

With this idea in mind, I took some measurements of the distances and hight of the seating position, location of sofa, etc and put this geometry into Fusion 360 – a CAD software. This allowed for easy determination of the correct height and angle for the speaker driver to be located, such that a reflection off of the wall would arrive at approximately ear level.

Diagram of sound reflection off of the wall. Red line shows the approximate reflection path.

A speaker driver was selected, meeting the criteria of being full range (not including frequencies that might be covered by a future subwoofer), relatively small, high sensitivity, 8ohm, and relatively inexpensive. Since I don’t have any test equipment (oscilloscope or calibrated microphone) I thought it would be best not to try for a two way speaker, since designing and testing the a crossover without being able to measure anything really isn’t engineering, it’s just guesswork. The sensitivity requirement was set at about 90dB/1m/1W since one of the speakers has a long and inefficient path including a wall reflection. Small drivers were required so that the speakers can remain compact. (In hindsight, a coaxial speaker might have been a good choice, as a I could probably find a sufficient crossover network that someone else has calculated.)

The speaker driver selected was the FaitalPro 3FE22. These are 8ohm, full-range speakers (~100-20k Hz) that have an RMS power handling of 20W and a sensitivity of 91dB/1m/1W. These would then be expected to play at up to 104dB/1m, which isn’t as loud as the front stage, but sure is enough to damage your hearing with extended play. Further, rear channels really don’t have much happening most of the time and so if slightly more power is pushed through them during the final blockbuster-explosion, then they probably won’t catch fire. Interestingly, in Dolby Pro Logic, the first one in the ’70s, the surround channels were mono and limited to 7kHz. Modern movie mixes use the rear channels more, but still most of the sound will always come from the front speakers, and lower quality rear speakers are a reasonable cost saving endeavour.

To design an enclosure you need to know how the speaker will perform. In the ’60s and ’70s Thiele and Small worked out a simple model of how speakers react in various boxes. Thiele-Small parameters are used to model speakers, although they only apply for low frequencies. Some speaker manufactures ‘fudge’ their numbers a little bit, so before I ordered the drivers I wrote a small C++ programme that checks the Thiele-Small parameters against one another (the parameters are not completely independent). The driver checked out and so I trusted the rest of their measurements.

In order to ensure that a solid 100Hz was playable through the speakers a ported box was designed in WinISD (a free speaker modelling software). WinISD takes the Thiele-Small parameters and plots the frequency response of the speaker in different enclosures. The TL;DR answer to speaker boxes is that larger boxes allow deeper bass notes to be played as the air behind the speaker is more easily compressed (just like a long piece of rubber band is more stretchy than a short piece). Ported boxes resonate, exactly like a mass-spring (or pendulum) system. Frequencies that are near to the resonate frequency of the port excite air in the port and cause it to oscillate, this boosts the volume at the port resonant frequency. If you align the ports resonant frequency to be about the same frequency where the speaker driver starts to loose efficiency (and so play quieter) then boosting the volumes extends the linear frequency range.

There are some disadvantages to ports, in that you are basically always listening to the driver as well as the delayed response from the port, these two pressure waves can interfere with one another, and can also extend the length of a note while the port is oscillating. Ports with a small area produce a chuffing sound as air rushes through them, and larger ports need to be very long to achieve the same resonant frequency, they also have a large mass of air that can cause them to be improperly damped. This being said, perfectly good speakers can be designed with ports – like anything in engineering there is a trade-off between whatever compromises you choose to make.

The compromise that I came up with was to have a large long port that slightly boosted the bass. Due to the method of construction, this very wide port was easier to make.

Comparison of a ported and sealed enclosure response in WinISD. The ported response has a higher -3dB point, but the response drops of more rapidly. The sealed box has a volume of 0.7L. The ported box has a volume of 2L and a 4″x1″ port that is 40.6cm long.

The final parameters for the ported box was a volume of 2L, a rectangular port of 4″x 1″ and 40.6cm long. With these parameters I then went back to Fusion 360 to design the boxes. I designed two completely different boxes that both have the same port length and volume. The first of which was a traditional bookshelf speaker form, with a front facing port. The driver height was set to be just above ear level. The second box was designed with the speaker driver angled at 5.7˚ above horizontal, and a plate such that it can be stabilised under a sofa. The second box was also much taller, just under the height of the arm of the sofa.

Designing a box of the correct volume is easy enough, working out the correct port length was a little more challenging, but for a folded port it is easy to use some algebra to work out how many turns to use. To make sure the speaker was stiff enough everything was made from 12mm MDF (although I understand that plywood would have been a better choice as it is stiffer for the same thickness), and the front baffle was made double thickness. The top of the angled speaker was also made twice as thick to reduce the radiated sound. The sharp angles in the port will cause turbulence and reduce the efficiency of the port – I assume it was also reduce the Q of the port resonance (which should increase the tolerance in port length).

Width of the baffle for both speakers was 4” (~102mm), I don’t have a table saw, and cutting many metres of straight 4” wood was never going to happen. Luckily my local hardware store was able to cut the wood for me. I planned the design around this so that my manual sawing would have the fewest opportunities to ruin the build. I only had to cut strips to length, and cut out the side panels.

I 3D printed a circle cutting jig for my router in order to cut the 3” hole for the driver; an M3 machine screw holds the jig to the wood and sets the radius. For small holes the order of operations is a little awkward as the screw head is under the body of the router. Rather disconcertingly when in use the last part of the circle is quite hard to cut as the wood is only joined by a thin section. I drilled the centre holes for the speaker cut outs with the two piece of wood taped together, however, the router bit was not long enough to cut through both piece of wood, so they were separated for the final hole. I cut the hole undersized for the driver, and, after gluing together both components, I widened the hole with a rotary tool to make room for the basket and terminals.

Wood cut to 4″ strips and marked for length.

The second speaker was much like the first. However, there were a few unusual challenges such as the angled joining points at the top of the speaker.

Front baffle with hole enlarged for speaker.

Test fitting the driver revealed the ideal location for the holes to fasten it to the baffle. I used M4 T nuts and machine screws to attach the driver as MDF disintegrates if screws are driven in and out of the wood. The drivers would have been difficult to flush mount, and already had gaskets on them, so this process was easier than it could have been. The T nuts were hammered in to the back, and later on in the build I used a clamp to seat them deeper as the first test fitting pushed them out (from the screw threading into the wood).

Each of the components were glued on to one of the side panels. 3D printed spacer cubes were used to hold the components of the port the correct distance away from one another. These were strong enough to clamp over and were printed very slowly so as to ensure they were dimensionally accurate. Clamps and weights (including a blender full of water) were used to hold everything together. Only one or two parts of the speaker were glued at each step, other parts were dry fitted in place to ensure everything stayed in position. Aluminium foil was used to separate surfaces that shouldn’t be glued.

The last part to be glued on was the side panel. The binding posts on both speakers were on the side panel as they were both designed to sit right up against a rear surface. Heavy gauge wire was soldered to speaker terminals and the binding post rings. The 3” hole for the driver was just large enough for my hand to tighten the nuts after the side was glued on.

I lightly sanded various parts of the speakers for fitting. The 5.7˚ angle for the angled speaker baffle was sanded into the front panel. And other parts were sanded flat to remove saw marks before gluing. The dust from this was collected and mixed with glue to make a wood filler that was used to fill the gaps made by my imperfect joinery. This filler was used inside and out of both speakers before the side panel was finally attached.

The two speakers were then installed in the living room, connected to the receiver. I manually set the distances and levels by playing white noise thought the each of the speaker in turn and using an app on my phone to measure the level– although at some point I should try the auto adjustment. The two speakers sound a little thin at the moment, but otherwise are fine. I have them set up as ‘small’ on the receiver, it then sends all of the bass to the front three speakers that have much larger drivers (the main speakers play down to 44Hz). I don’t know if this is the best compromise. Maybe I’ll update this when I’ve lived with them for a little while.

Surround music sound really good on the system with Dolby Prologic II music. This algorithm takes normal stereo music and sends the common signal to the centre channel and the difference between the left and right to the rear channels with some filtering. You get some interesting ambient effects and it really feels like the music is surrounding you. I’m sure better rear speakers would make it sound even better, but I’m quite happy for the moment with these. (You can do a similar thing without any fancy processing with a spare speaker and any normal stereo. Just connect the spare speaker to two positive terminals of your amplifier i.e. the positive from the left speaker and the positive from the right speaker. Then run that speaker behind you. The stereo sound should be about the same, but ambient effects will play through the rear one (you can do the same with two rear speakers). This set up is called a Hafler circuit, the ambient sounds that you hear are sounds that are out of phase between the L/R speakers.)

Movies also sound really good too. The first film we watched with the speakers installed was Jurassic Park, incidentally the first film with a DTS sound track. I was particularly struck with the echoes in the entrance hall of the Jurassic park building. In a darkened room, you really feel like you are in a room the size of the one depicted, not the size of your own room. The fire work effects in Coco were also very involving as you can hear them all going off around you.

First on my list of things to finish off with them is to get some primer on. The MDF won’t last long without something to protect it. However, that will involve quite a bit more sanding and a few clear days when I can paint outside, and then the final colour can go on. After that, I’d like to measure the output of the speakers and see if I can improve the sound. I have some DSP capability on the amplifier, but I might also try to implement a baffle step correction circuit.

In short, if you don’t have room to put a speaker for a surround sound system. You really can bounce the sound off of a wall, and it sounds pretty good.

So… We built a robot.

Projects, Robots

I used to love robot wars when it was on TV. I always wanted to make a robot for the competition, but when I was a kid I didn’t have the technical skills or budget to make a 100kg fighting robot. I still don’t, but more recently my girlfriend and I found out that there are several weight classes of robot which people compete in the UK, one of them is the 1.5kg ‘Beetleweight’. These are much more affordable and safer than the heavier weight classes. So we immediately started planning out a design for Seven of Nine Lives.

If you have any background in physics/engineering the benefits of spinning stores of energy are obvious. The energy stored is proportional to the square of the angular speed of the blade. Effectively, you charge a battery over an hour, and then dump energy from the battery into the spinning weapon over 10sec and then you dump that energy into the other robot in ~1/1000th of a second. Even with 1.5kg robots the energy storage in the weapons can be quite amazing, many times the energy of a bullet.

Anyway, our approximate plan is for a light, small, sturdy robot with a huge bar spinning on the top. Currently we have a 3D printed draft of the design. This current prototype is the first version of the robot in which all of the components work. It drives around well and the weapon spins up.

We had a lot of problems with the drive for the weapon. This stalled the development of the rest of the robot for quite a while as we thought we had damaged the motor/ESC (electronic speed controller), but it might be that we were using the wrong kind of drive belt (we used a beefy V-belt). This is next on the list of things to fix, but currently, we just have the weapon directly mounted onto the motor – clearly not a good idea as the bearings inside the motor are not designed for any side loads – but as the weapon is made of hollow plastic at the moment it doesn’t seem to be an issue.

We have spent many nights researching, planning, designing, soldering, and constructing this prototype. It’s been really interesting so far, but we have a lot more work to do. After we sort out the drive for the weapon we can start working out how to make the chassis out of aluminium. It would be really interesting to numerically model the performance of the weapon, armour, and chassis but that seems to be a little out of our area of expertise. If anyone has any tips for this kind of simulation we’d be very interested. So far we have just used the simulation module in Fusion 360, but it seems to be designed for static loads or resonance conditions.

Seven of Nine Lives driving around and attacking a plastic bag. If any opposing robots use plastic bags as armour they will likely be defeated.

The Humble Tessar

Optics, Photography, Projects

In April 1902 Paul Rudolph, of the Carl Zeiss firm, applied for a patent for a camera or projection lens:

‘[Constructed by]… arranging four single lenses in two groups separated by the diaphragm, the two components of one of the groups inclosing an air-space between their two surfaces, facing one another, while the two components of the other group are joined in a cemented surface, and the pair of facing surfaces having a negative power…’

The full specification of the lens is included in the patent, but the wording is extremely broad. The Tessar is considered to be any lens of four elements, with a doublet and a pair of singlets. However, Rudolf Kingslake in The fundamentals of lens design gives more insight, describing them as like Protars but with an air-spaced front group, the Protar being another design from Rudolph and produced by Zeiss from 1890.

If we want to swap out those refractive index values for Abbe values we can simply fit Cauchy’s equation and use that to estimate the C-line index, giving the table below.

Simply fit the three wavelength/index pairs to Cauchy’s equation to calculate the missing values. Only the first two terms were needed.

	nd (589.3nm)	Vd	∆P(g,f)
Lens 1	1.61132	58.4128	0.020117
Lens 2	1.60457	43.2243	0.012310
Lens 3	1.52110	51.5109	0.013207
Lens 4	1.61132	56.3675	0.021767

Refractive index Abbe number and anomalous partial dispersion for the glasses listed in the Tessar Patent

The original patent lists most of the values needed to model and construct the lens, however, you might struggle to find those particular glasses. A more modern formulation, from Kingslake, would find the same basic lens updated with modern (for 1978 in the case of my copy of lens design fundamentals) glasses, SK-3, LF-1, and KF-3, of note is the significant decrease in index of the second lens, but still flowing the same idea of a dense crown for the outer elements and medium flint for the second, and a light flint for the third.

The system focal length seems to be nominally 1000mm and back focal distance is 907mm. For the purposes of this exercise the presented designs will be scaled to exactly 1000mm focal length.

The lens produces an image circle of approximately 500mm. Requiring good performance over this size field is a challenge, but would be necessary if the camera was intended to be used without an enlarger. However, if only contact printing was intended then the definition requirement would be significantly lower. If the camera was to be used with wetplates then the chromatic aberration requirements become quite challenging, as the camera needs to be corrected for longitudinal chromatic aberration in the visible light (where it is focused) and the near-UV where most of the exposure comes from.

My initial hope/plan was to simply re-optimise this lens with modern computer optimisation and to get a slightly better performing lens at f/4 over the f/5.5 lens. This did not happen. It seems that Zeiss’s reputation was well earned. However, what I did do was significantly alter the lenses character and learn a lot on the way. For one, I didn’t really understand the importance of vignetting for aberration control, as you can clip off some of the problematic rays near the edge of the field of view, with only a small loss in edge illumination.

We can assess the performance of a photographic lens in a number of ways. From a design point of view one of the most obvious is spot size. This is the size that a single point of light would make at the focus of the lens. Different object distances can be considered, but for this I only looked at objects at infinity. Lenses tend to have better definition in the centre than at the edge, so it is important to examine the spot size at different field angles. Also, since lenses have dispersion it is important to also examine the effect of wavelength on the system. I used three main methods to judge image quality, the polychromatic spot size, chromatic focal shift, and image simulation. The image simulation also gives an idea of the performance of the whole system, including sharpness, chromatic aberration, and vignetting.

Layout of the Patent version of the Tessar, at f/5.5.

Raytrace of the Patent Tessar, at f/5.5.

Chromatic focal shift in the Patent Tessar. The maximum focal shift is 916µm

Spot diagram for the patent Tessar at 0˚, 7.5˚, 15˚, 20,˚ and 30˚ at f/5.5. The colours show the wavelength.

There are some things we do know about the lens such as properties of the glass and the radii of the curvatures. But there is also other information which we don’t know, such as the semi-diameters of the lenses, or the manufacturing tolerances of the system. If we guess at the first and ignore the second we can model the system as shown in the figures. The rear lens group is slightly smaller than the front group, vignetting some of the rays – this is set by the edge thickness of the rear lens.

To characterise this lens we might say that it is well optimised over the whole field, with the spot size increasing by more than a factor of 3 from the centre to the edge. The chromatic shift isn’t significant and at f/5.5 there isn’t any obvious lateral chromatic aberration.

I re-optimised the lens several times, tweaking the weightings of various factors. I decided that distortion wasn’t an issue, and that over-all central performance was more important the edge or the very centre. I also kept the same glass as the original. The prescription which I arrived at is

	Radii/mm		Thickness/mm
r1	213.366	L1	40.881
r2	-3276.842	gap	19.710
r3	-648.011	L2	11.081
r4	197.148	to stop	39.115
r5	-777.429	from stop	19.649
r6	221.080	L3	8.382
r7	-340.573	L4	46.140
		Backfocus	887.795

Re-optimised prescription for lens

As can be seen from the table and the layout diagram the first lens of the re-optimised lens is almost unchanged. The second lens is slightly strengthened on both surfaces. The rear doublet is thickened and has more power. This might have been avoided in 1902 due to the cost of the ‘new achromat’ glass. Overall, the lens is not much changed, at least by examination. I expect that the 1902 patent lens would be less expensive to make due to the weaker surfaces and thinner lenses. However, in the re-optimisetion I did squeeze an extra stop of speed out of the system.

Raytrace of the re-optimised Tessar at f/4

Focal shift in the re-optimised Tessar, maximum focal shift is 766µm

*Spot diagram for the re-optimised Tessar at 0˚, 7.5˚, 15˚, 20,˚ and 30˚ at f/4. The colours show the wavelength.*

The re-optimised Tessar is a slightly better achromat with a smaller maximum chromatic focal shift of 766µm instead of the 916µm of the original Tessar. This is probably not significant. I don’t know exactly how the original lens was achromatised, however, my choice was to achromatise 0.54µm and 0.4861µm. These value were chosen as they are close to the peak sensitivity of the eye and of the collodion process, hopefully, a photographer could focus in the visible light and expose with minimal focus shift in the blue/near UV.

In the spot diagrams of the re-optimised lens you can see an obvious design choice, the centre spot has been allowed to increase in size slightly, and the very edge spot has increased significantly, all of the other regions show significant spot size decreases. This is due to a difference how I would personally like to compose images, with a less strong centre bias than 1902-Zeiss expected.

The average spot size for the re-optimised lens is significantly larger than for the patented example although almost all of that is in the very edge, but we can’t judge it too harshly as the re-optimised version is almost a stop faster at f/4 rather than f/5.5. If we stop it down to f/5.5 we get a slightly different result.

Raytrace for the re-optimised Tessar, at f/5.5.

*Spot diagram for the re-optimised Tessar at 0˚, 7.5˚, 15˚, 20,˚ and 30˚ at f/5.5. The colours show the wavelength.*

The spots have decreased significantly over the field when stopped down, as would be expected. The central spot size is now almost the same as in the patent design, and the 15˚ spot size is now smaller than the 7.5˚ spot size in the patent design – this significantly increases the region of good definition of the system.

Perhaps a more meaningful way of comparing the lenses is by simulating an image made from them.

Comparison of the image quality between the original patented Tessar and an re-optimised version of the lens.

Examining the simulated image (which doesn’t take into account depth) we can see some of the character of each lens. Like with any other artistic tool, the final judgement is based on the desired use.

The actual imaging properties of a real Zeiss Tessar lens (a 1960s Carl Zeiss Jena Zebra Tessar 50mm f/2.8) are analysed in this post.

Circle packing

Projects

Circles are ubiquitous in nature as they minimise surface for a given area. Circles arrange themselves in efficient ways due physical forces – lipid vesicles inside cells for example. The patterns look pretty cool too.

Randomly generated circles in a range of acceptable radii

There are several simple circle packing algorithms which can be used to generate these patterns. A central requirement in many of these algorithms is determining if a given circle is wholly outside of another circle. This can be simply calculated by requiring the centre of the new circle is at least separated from the old circle’s centre by the sum of the two radii. A simple circle packing algorithm then randomly generates centres and radii and tests to see if these are wholly outside of all of the current circles. This algorithm produces more small circles.

Initial large circle with smaller circles generated around it.

It is then simple to add other requirements and initial conditions. Large circles can be used to produce negative space around which the other circles can be distributed.

The packed circles can be filled in a variety of visually interesting ways.

Circles above a certain size are not drawn

Controlling the drawing process is also interesting, smaller concentric circles can be draw inside larger ones, or some class of circle can be skipped out.

The images produced are typically visually complicated. Simplifying them or adding order can significantly change the nature of the image.

To take this process further, more efficient packing and drawing algorithms could be implemented, as could more filling techniques (lines, zigzags, spokes) and colours. Further, generating these patterns could be generated according to the intensities of a photograph.

A pair of new related sequences of integers

Projects

A) 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 2, 2, 1, 2, 1, 4, 1, 1, 1, 1, 2, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 2, 1, 4, 1, 1, 1, 2, 2, 1, 1, 1, 5, 1, 1, 1, 1, 1, 3, 3, 1, 3, 1, 1, 1, 7, 3, 1, 1, 1, 2, 1, 2, 1, 1, 1, 2, 1, 1, 1, 1, 3, 1, 1, 2, 2, 1, 3, 2, 2, 1, 4, 1, 1, 2, 2, 1, 1, 2, 1, 1, 2, 1, 3, 2, 2…
and
B) 1, 1, 1, 1, 1, 1, 1, 2, 5, 3, 1, 1, 1, 1, 2, 1, 2, 1, 3, 1, 1, 1, 1, 3, 1, 3, 3, 3, 4, 1, 2, 1, 2, 3, 1, 2, 1, 1, 1, 2, 1, 1, 1, 3, 1, 1, 1, 3, 3, 2, 3, 3, 1, 1, 5, 4, 3, 2, 3, 1, 7, 3, 3, 1, 1, 2, 1, 1, 1, 2, 2, 1, 2, 1, 2, 3, 1, 2, 3, 4, 1, 1, 1, 1, 2, 1, 5, 3, 1, 1, 3, 2, 3, 1, 3, 3, 4, 1, 4, 1…

What are these sequences, and what links them? Well, if you take the prime numbers in order, and sort each of their digits and then count how many factors each of these numbers has you’ll find either sequence A or sequence B depending on if you sorted the digits highest first or lowest first. The 1s represent numbers which are primes. The first few prime numbers only have 1 digit, so sorting the digits gives the same number, then there is 11, which sorted is still 11, and 13 which can be sorted to 13 or 31, both of which are prime. 19 is the first prime number, which when sorted highest to lowest gives a composite number.

A property of this pair of sequences is that, at least up to 9592 digits, the sum of the first n digits of B is greater than A. This is expected as the intermediate values, the sorted prime digits, of B are 1 larger and 2 more likely to have 0s or 2s at the end of them (since 0 and 2 are both small numbers and guarantee numbers to be composite). Larger numbers are more likely to have more factor since there are more available combinations. I don’t know this result to be true for all N, it is a conjecture.

I’m hoping that the sequences get accepted to the Online Encyclopedia of Integer Sequences (OEIS) which is the goto place for sequences like this to be sorted so that people can cross reference. If they do get accepted then they’ll be sequence A326952 and A326953, respectively. However, the OEIS curates the sequences that they list carefully so as not to include arbitrary sequence which no-one else will find interesting. I don’t know if other people will find this interesting.

Excitingly, as of the 25th of August, they have both been approved https://oeis.org/A326952 and https://oeis.org/A326953

Plot of the cumulative sum of each of the sequences

Plot of sequence A against sequence B for the first 4796 terms

Computer Controlled Macro focusing rail

Macro Photography, Photography, Projects

Stack of 128 frames of a wasp using a 3.7x 0.11NA objective on a Pentax K-1

Focus is often used creatively in photography to separate the subject from the background of an image. In microscopy ‘optical sectioning’ to resolve details out of the plane of the image. In macrophotography, however, we often want to capture images which are pin-sharp front to back. Doing this is quite hard.

The depth of focus is very narrow at high magnification. In fact, in the wasp portrait the depth of focus was only 58 microns, or only 0.058mm. You can see what a single image looks like bellow. Only few hairs are in focus. In total for this photo I took 128 images in 20 micron steps.

It’s pretty hard to move in 20 micron steps by hand, so for a little while I’ve been putting together a focusing system.

Version 1 was just a z-axis rail for a CNC machine. A rail with a carriage supported on it, with a screw thread and a like-threaded insert on the carriage, and a stepper motor. This was controlled by an arduino and stepper driver. The camera was set up with an interval timer, and the arduino code had periods in it for the camera to take a photo.

This setup had several disadvantages, securing the camera to the camera was difficult. an M5 to 1/4″ bolt was used, but this didn’t allow for the camera to be securely fastened. Also, the minimum step size was ~50µm which wasn’t fine enough. Lastly, the camera needed to stay in sync with the arduino, which was achieved by starting the arduino code a few seconds before the camera, not ideal.

Version 2 has a number of improvements. By cannibalising a shutter release cable I’ve been able to control the camera from the arduino, by just bringing a pin high. I also drilled out a tripod base plate to give sufficient clearance for the camera plate to slide into it, while everything is bolted together. Lastely, I swapped out the threaded rod for a M8 fine pitch rod. This rod has a pitch of 1mm, and only 1 thread cut into it, instead of the ~2.5mm pitch and 4 threads cut into the rod I was previously using. This improves the stepping precision by a factor of 10. A single step on the new system is only 5µm, which is only about 10 wavelength of light.

The thread was cut into a small block of wood which was pre-drilled with an 8mm hole. The wood offers quite a lot of resistance, but also doesn’t produce any backlash.

1:1 zoom of the eye of the wasp. 1px is 1µm in size. The facets of the compound eye are most interesting as they transition from the hexagonal packing into a square packing.

Mounting unusual lenses on digital cameras

Macro Photography, Photography, Photography Equipment, Projects

*lens recovered from Polaroid Sprintscan 35*

Pleasing effects can often be found when using unusual lenses on modern digital cameras. Sometimes they give a highly aberrated image which is useful in creative situations, sometimes the history of the lens enhances the image in a meaningful way, and sometimes the unusual lens offers a quality which is not possible with typical lenses from first party manufactures.

The last instance is often the case with macrophotography. Many people use objectives to photograph small insects as they offer much higher magnification ratios and resolution than macro lenses. Occasionally, lenses used for obscure purposes in industry can find use in various areas of photography. Surplus aerial photography lenses, such as the Kodak Aero-Ektar are highly sought after for their high resolution and high speeds over large flat film planes. Occasional lenses with have excellent performance are found for macrophotography.

It is one of these which I have acquired recently from an old film scanner. Film scanners image a flat sheet of film onto a flat sensor at high resolution. Unlike lenses for general photography they are optimised for magnification ratios of around 1. Most photography lenses are optimised for a magnification of almost zero.

Mounting a lens can be easy. Adapters often exist allowing a camera lens to be mounted on other cameras. However, when we look at older lenses, or lenses which were designed for industrial use the adaptation is more difficult.

In order to mount the lens securely, I designed a small device to securely hold the lens. The bore has 0.5mm of clearance for the lens barrel, and a flange at the base so that the lens can be reliably positioned the same distance from the sensor. This was 3D printed by a friend of mine. There is also a place for a grub screw to be installed so as to secure the lens in place. The base is so sized so that it may be bonded to a body cap. The injection moulding used on the body cap left the inside surface shiny, this was sanded to reduce reflections. The body cap can the be fitted to a set of bellows or extension tubes.

*3D printed lens hold affixed to body cap and with a screw to hold the lens in place*

Lens mounted to an old set of bellows. These bellows are backwards, so that the remaining rails are on the camera end.

I was surprised to realise that the top of the body cap was quite convex. This cased two problems. Firstly, the contact area which the lens holder made was rather small, and secondly, it would slide about as the glue dried. To compensate for the first issue I used quite a lot of adhesive. To compensate for the first I used a quick curing epoxy resin. This turned out not to be so quick curing, and I spent about 30 minutes poking the parts into alignment.

I intend to test the lens both ways around and at different magnifications. I don’t know exactly what magnification it will perform best at, presumably at it’s design magnification. However, it may surprise us. The lens is not a symmetric design, the front (dot end) has a convex element, the rear surface is plano.

I took the lens out for a short while and tried to photograph some insects. Unfortunately, I didn’t bring my flash light guide, so most of the picture turned out greatly under-exposed. The lens is not exceedingly sharp, at least, not at the magnifications which I tested it at. However, this is not a well designed resolution test (that will come later).

Full image (resized) and 100% zoom on a 36MP full frame sensor

As can be seen from the above frame, the lens is not sharp to the pixel. However, it shows nice contrast and has very little longitudinal chromatic aberration.

Not many insects would stay still for me. This guy did, but he was really small.

The insect above was very small. I’d be interested to know what species it is. Part of the issue with this photo is the due to a heavy exposure pull due to a lack of flash power. The Pentax K-1 isn’t known for its dynamic range, but this is pulled 3.5 stops, and I don’t think it is so bad. I tried a few different magnifications, but I didn’t keep track of it. The working distance is quite short, but this is also a lot higher magnification than my macro lens.

The resolution is probably what I should expect. The scanner that this lens came from was a 2,700 dpi scanner and the resolution of my sensor is 5,200 dpi, so it isn’t surprising that the sensor out resolves the lens. However, image space resolution isn’t the only important property.

Linify: photographs to CNC etch-a-sketch paths

Projects

Linify: def. to turn something into a line.

I saw someone the other day using a variable density Hilbert curve to transform an image so as to be projectable using a laser and galvo mirror setup, this was on the facebook page Aesthetic Function Graphposting.

That kinda stayed in the back of my mind until I saw This Old Tony’s youtube video about making a (computer numeric controlled) CNC etch-a-sketch. The hardware looked great, but he was just using lame line sketches of outlines, the kind of limited images which you’d expect from an etch-a-sketch.

So, I put together a lazy easy way of turning a photo into a single line. Here is an example of my face. If you move quite far back from the image, it looks pretty good.

It uses a variable amplitude sinewave patches, which have a whole number of periods. Sine waves are used due to their simplicity and their periodicity. The same effect could be achieved with other periodic waves, in fact, square waves may be more efficient for CNC applications, as fewer commands would need to be issued to the orthogonal control axes.

The image is first downsampled to a resolution around 64 px on an edge. Then, for each pixel in the downsampled image, an approximate sinewave is found. Blocks of sine waves are added to a chain, which runs over the whole image. Currently, it raster scans, but it would be pretty easy to go R->L on even and L->R on odd. To improve the contrast, the downscaled image is contrast stretched to the 0-1 interval, and then each intensity value is raised to the (default) power of 1.5, this gives a little more contrast in the lighter regions and compensates somewhat for the low background level and the non-linear darkening with greater amplitude. This could be tuned better.

There are several factors which alter the contrast. The cell size, frequency, number of rendered points, linewidth, and also the gamma-like factor applied to the image before the linify. Images were then optimised by adjusting the gamma-like factor. Optimal values were found between ~0.75 and ~1.65. Higher values were better for darker images. Successive parabolic interpolation (SPI) was used, four values were selected at random, and their error with respect to the original image was found. These values were then used to fit a parabola, and the minima of the parabola were used as a new point. This process was iterated with the four best values being used for the fit. This process can be seen in the figures below. In the first figure, four points (the blue stars) are found. The first parabola is fitted, and the red point is the predicted best parameter value. In the second figure, the blue star shows the true value of the metric we are trying to minimise, it is slightly different than predicted. A new estimated best parameter value (green) is found. And so on. To ensure that the parabola is only used near the minima of the function, the points farthest from the minima are discarded. Typically, only three points are used, my implementation uses four for robustness, which is helpful as the curve is non-analytic and non-smooth.

A few starting locations were checked to ensure that the minimum found was global. This kind of root finding, SPI, is very simple and commonly used. It converges faster than a basic line search (about 33% faster) but does not always converge to the local extremum. Parabola are used, as the region around any minima or maxima of any function can be approximated by a parabola, which can be observed by the Taylor expansion about an extremum.

Whilst we have a non-linear intensity response and some artefacts from the process, it is much easier to get this kind of process to well represent real images than the skittliser process, as we have a wide range of possible intensity levels.

Of course, one of the issues with using this method on something like an etch-a-sketch is the extremely long paths taken without any kind of reference positions. Modifications could be made internally to an etch-a-sketch to have homing buttons which would click at certain x or y positions, thus giving the control system a method of resetting itself at least after every line. A much more difficult, but potentially interesting closed-loop control system would be using information from a video feed pointed at the etch-a-sketch. Taking the difference of successive frames would likely be a good indication of the tip location.

Finally, here is a landscape photograph of a body of water at sunrise. Just imagine it in dusky pink.

Joshua McBruceer

Photography and Projects

Projects

I Hacked an ECG Machine

Decoding the ECG Signal

Zeiss Tessar: How does my vintage lens blur images?

DIY wall-reflecting surround sound speakers

So… We built a robot.

The Humble Tessar

Circle packing

A pair of new related sequences of integers

Computer Controlled Macro focusing rail

Mounting unusual lenses on digital cameras

Linify: photographs to CNC etch-a-sketch paths