Zeiss Tessar: How does my vintage lens blur images?

Computer Vision, Optics, Photography, Projects

Modern camera lenses are typically super sharp but can sometimes lack character. Vintage lenses with fewer corrective elements are typically softer and have decreasing contrast and resolution in the corners. But what’s going on in my lens?

In this post, I’ll use computer vision techniques to analyse the performance of this vintage lens and then see what effect this has on photographs.

Lens adapted onto modern mirrorless camera

Background

The lens was a budget product from one of the premier optical manufacturers in the world, Zeiss. Zeiss has long been synonymous with excellent optics, developing many key technologies in its history. Currently, Zeiss produces extremely high-performance optics for a range of applications, including photography and photolithography – the silicon chips in your laptop and iPhone were likely manufactured using Zeiss-made photolithography systems. After the partition of Germany, Zeiss – a high-tech company critical to modern economies and militaries – was also partitioned. Much of the stock, equipment, intellectual property, and staff were taken by the Soviet Union to kick-start its optics industry and the remaining Zeiss company was split into Zeiss Oberkochen in West Germany that largely sold to the West, and Carl Zeiss Jena in East Germany that largely sold to the Soviet Union.

This lens was manufactured in 1967 by Carl Zeiss Jena and is a Zeiss Tessar design. The original Tessar was patented in 1902 which I have previously discussed, but this one was redesigned for smaller formats using the latest glasses and design techniques. It was sometimes called the eagle eye because of its centre sharpness and contrast. This is a 4 element/3 group design that performed well, especially when coating technology was in its infancy when it was important to minimise the number of glass-air interfaces to reduce flaring. This example is single-coated, has a minimum focus distance of 0.35m, uses unit focusing (the whole optical unit moves back and forth to focus), and was designed for use with 135 (35mm) film probably for colour and black and white – which were both available when this lens was manufactured. Films available in 1967 were very different to the ones available now and in the ’90s. They were slower and had more grain, Kodachrome II (I believe the most common colour film available in 1967) was available in ASA 25 and Kodachrome-X had just been released in 1962 with a speed of ASA 64. ASA speed is basically the same as ISO speed – in fact, ASA and ISO are just standard agencies (American Standards Agency and ISO kind of means International Standards Organisation, although it now isn’t an acronym and is just ISO, the Greek prefix for same) which specify how the film speed should be measured, there are ISO standards for bolts, paper sizes, and almost anything else you can think of (including how to make a cup of tea).

The lens has a five-bladed aperture, aperture clicks from f/2.8-f/22 with half stops. It has a depth of field scale, infrared focus mark, and an automatic aperture system – meaning that, on a compatible SLR, the aperture remains open for focusing and then stops down the specified setting when the shutter is depressed. It uses the M42 mount which is easily adapted to other systems due to its long back focal distance. The lens body is made of aluminium and has an attractive brushed/striped design that offers excellent grip. This particular lens had a stuck focusing helicoid, so I removed the old grease using lighter fluid, lint-free paper, and cotton buds and re-greased it with modern molybdenum grease (Liqui Moly LM47).

I wrote some software (this actually took ages) and printed off some test charts to work out exactly what my vintage Zeiss Tessar 50mm 2.8 lens is doing to my images.

Analysing the Blurring

I photographed the test charts at a set distance (0.6m) wide open (f/2.8) and stopped down (f/8). The camera was set on a stable tripod and carefully aligned so that it was perpendicular to the floor where the test chart was placed a 10-second shutter delay was used to reduce camera shake and the camera was set at its base sensitivity to minimise noise.

The software that I wrote found each of the test targets in the stopped-down image and found the corresponding test targets in the wide-open image, this is shown in Figure 0. I then assumed that the stopped-down image was perfect and used it as a reference to compare the wide-open image.

Figure 0. Computer vision algorithm automatically finds the targets in the test chart.

Using some fancy maths (called a Fourier transform) you can work out how to transform between the sharp stopped-down image and the blurred wide-open image. I did this for each target on my test chart because the amount and nature of the blurring are different across the frame.

Fig 1. Reference test chart taken at f/8 with centre and edge targets marked. The edge targets are less sharp than the centre even in the reference image.

Fig 2. Wide open test chart taken at f/2.8 with centre and edge targets marked

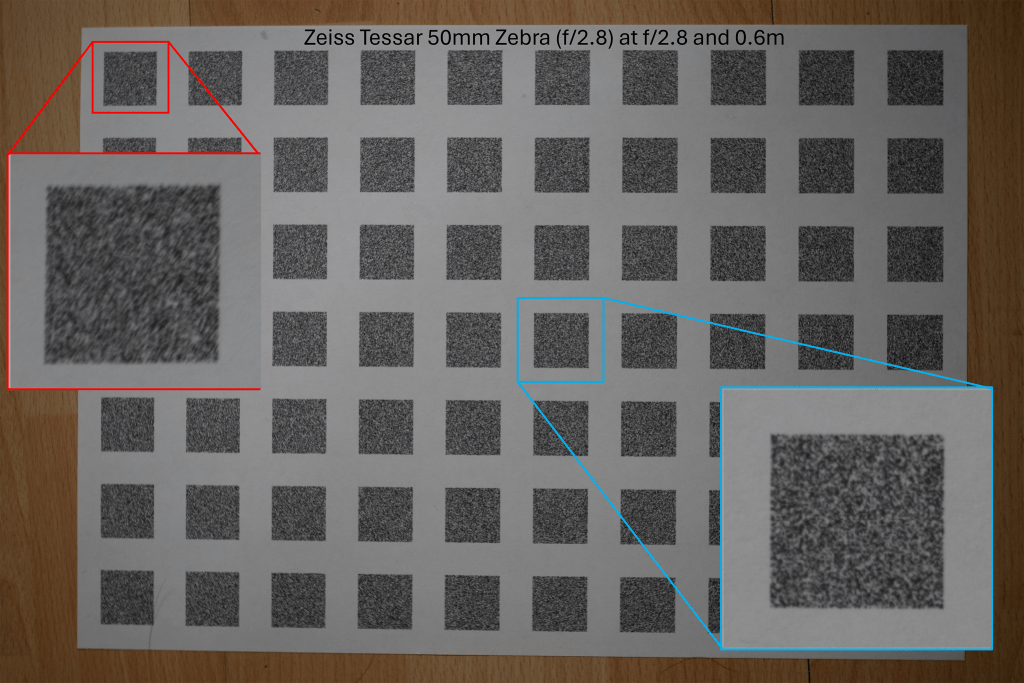
The above images are the photographs of the test charts photographed at the sharp aperture (f/8) and the blurred aperture (f/2.8). This method of using the sharpest aperture of the lens as the reference was used because it allows for perfect alignment of the images – both images have the same geometric distortion. A limitation of this method can be seen in Figure 1 in which the corners of the image are not perfectly sharp even at f/8. I was inspired to use this method after reading the excellent paper High-Quality Computational Imaging Through Simple Lenses by Heide et al, 2013, although the actual method that I used was different.

Fig 3. Comparison of reference and wide open targets. The central targets are slightly blurred and the edge targets are very blurred.

Enlarged examples of the test target pairs are shown in Figure 3. I then worked out exactly what blurring function you need to apply to the sharp image to produce the blurred image for each pair of targets. The result of this is shown in Figure 4, which is an array of point spread functions (PSFs). These PSFs show how each point in the image is blurred by the lens – the PSFs in Figure 4 are zoomed in 7x. Figure 4 also includes a second array of targets that is offset from the one shown in Figures 1 and 2, that’s why the PSFs are arranged in two grid patterns. The results from the two test charts agree.

Figure 4. Point spread functions at different locations over the frame. Zoomed in 7x

Figure 5. PSF from the centre of the frame. The PSF is compact with a halo around it that is mostly symmetrical. Left is the original and the right panel has increased contrast.

Figure 6. PSF from the centre of the frame. The PSF has a core and a surrounding extended diagonal line. Left is the original and the right panel has increased contrast.

Figures 5 and 6 show enlarged PSFs from Figure 4. The nature of the PSF changes over the image. The PSFs in the centre are more compact and have a distinct halo around the central region, an ideal PSF would have a central point and no surrounding detail. The halo around the points is spherical aberration, this is an optical aberration caused when rays parallel to the optical axis of the lens are focused at different distances from the lens depending on the distance from the optical axis. This causes a glowing effect in the image, since a sharp image is formed (the sharp central core of the PSF) and a blurred image of the same object is also formed but superimposed on the sharp image. This would not greatly reduce resolution but would reduce contrast. Spherical aberration should be constant over the image frame, but varies a lot with the aperture size used in the lens, stopping the lens down reduces spherical aberration quickly.

The PSF in Figure 6 mostly shows sagittal astigmatism. Astigmatism is when rays in two perpendicular planes have different focal points. Two kinds of astigmatism that occur in systems like this are tangential astigmatism and sagittal astigmatism. Tangential astigmatism points towards the optical centre of the frame and sagittal astigmatism points perpendicular to the centre of the frame. Sagittal astigmatism can cause a swirly effect in images as it blurs points into circular arcs around the optical centre. A lens with sagittal astigmatism can be refocused to give tangential astigmatism so the orientation of the astigmatism will flip around. This is because the best sagittal focus and the best tangential focus occur in different planes. Astigmatism doesn’t occur in the centre of the frame and increases rapidly towards the edge of the frame and with increasing aperture size. This aberration is sometimes called coma which is a similar but distinct aberration that looks a bit like a comet with a sharp point pointing towards the centre of the image and a fatter tail pointing away.

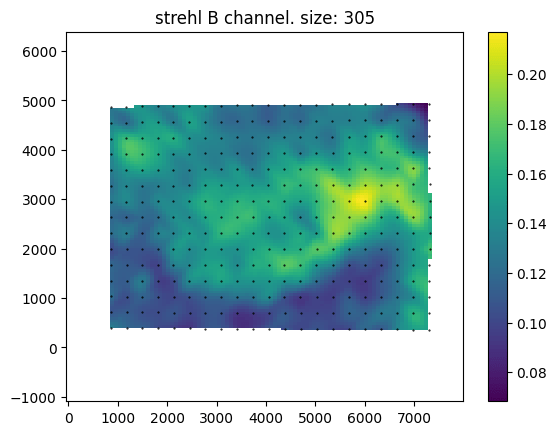
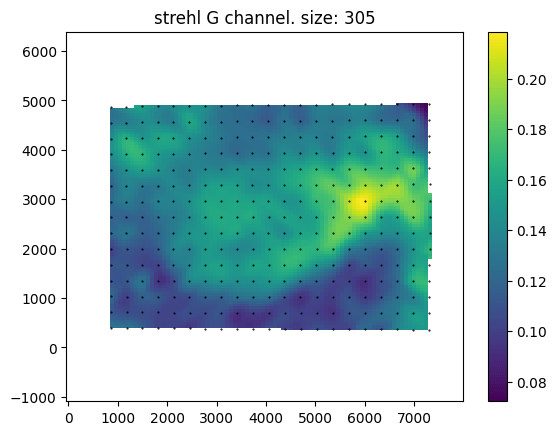
Above are maps of the Strehl ratio of the PSF. Strehl ratio is a simple measure of PSF quality, where higher values (maximum 1) indicate that the PSF is most similar to an ideal PSF e.g., a single point in this case. The bright greens are the regions of highest sharpness and the dark blues are the regions of lower sharpness. There is likely some noise in this estimate – I don’t completely trust it. However, from this analysis, it seems that the lens is somewhat decentred, as the sharpest region of the lens is not in the direct centre. This could be due to manufacturing defects such as the lens elements not being correctly seated, or due to damage that occurred during the previous 57 years, or due to an alignment issue with the lens adapter or the target was photographed.

An interesting feature of this lens is the apparent lack of axial chromatic aberration. The PSFs are very similar in each colour channel and the Strehl maps are also very similar, these tests are not very demanding and are not able to test at all for transverse chromatic aberration. For a lens likely designed with black and white photography in mind this is a pleasant supprise.

Example Images

Below are sample images taken with the lens at various apertures, mostly f2.8 (wide-open) and f/8. The second gallery includes zoomed-in regions to show the character of the lens in more detail. Simple colour and exposure correction was applied in Adobe Lightroom, no texture, clarity, or dehazing was added. Images were resized to 1600px on the long edge with sharpening for screen added at export.

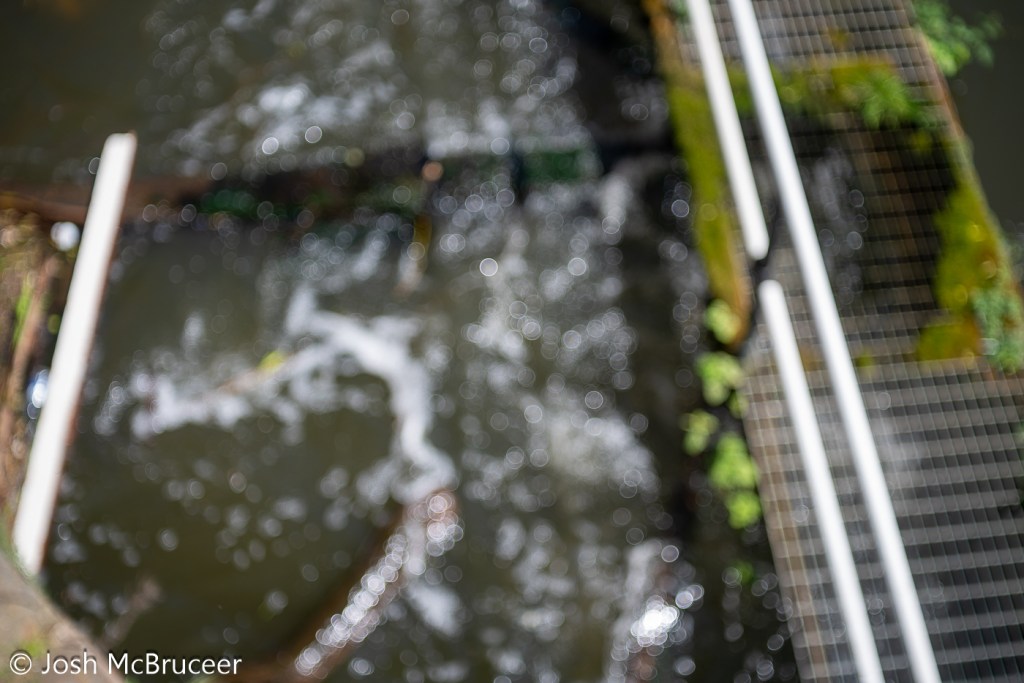
A selected sample of images with zoomed-in regions. The image with daisies shows much greater sharpness in the centre of the image compared with the edge and some swirling effect caused by the astigmatism in the lens. The pair of images of the graffiti rabbit (f/2.8 and f/8) show the increase in contrast and sharpness as the lens is stopped down. All areas of the image show an improvement in sharpness and contrast, but the edges improve more. This is also shown in the pair of leaf images, however, the increase in depth of field in these images makes it harder to determine sharpness changes in the plane of focus. The train track images show the same trend with a distinct increase in contrast in the centre of the image (the clocktower).

The bokeh image is of running water in a canal and was taken with the lens set to close focus at f/2.8. The bokeh is bubbly with distinct outer highlights which indicates over-corrected spherical aberration, sometimes this is considered attractive such as in the Meyer Optik Goerlitz Trioplan lens, however, the effect is less strong in this Tessar. This also leads to the distracting out-of-focus elements in the last image of the dog (my beagle, Saturn) where a line out of the plane of focus is blurred into a sharply defined feature.

None of these images show chromatic aberration, this would likely be apparent on the image of the tram powerlines.

f/2.8 red lines showing the direction of the blurring causing the slight swirl effect.

Conclusion

Despite the lens being 57 years old it is still capable of producing sharp images. The lens is sharper in the centre of the frame than at the edge and the edge has a small amount of swirl effect. The lens doesn’t offer much ‘character’, which is likely expected as it was a standard lens for decades and most people want low-cost, small, sharp-enough lenses that don’t detract from the subjects being photographed. There some pleasant aspects of the lens, such as the slightly soft look that may be pleasing for some portrait work, and the bubbly bokeh may be desirable for some creative effects.

To get the most character from this lens, have a bit of separation between the subject and the background and foreground elements. Strong highlights may have a distracting or exciting bubbly effect, so stay cognisant of this. The lens has a great minimum focusing distance and so can produce quite a lot of out-of-focus blurring, it’s also a bit softer up close, so use this when you want to knock out very sharp details, such as skin texture in portraits. The lens has little chromatic aberration so don’t worry too much about that. The vibes of the lens tie the image together nicely, although they make it a little flat before contrast is added back in editing.

JPEG artifact removal with Convolutional Neural Network (AI)

Uncategorized

JPEG images, at high compression ratios, often have blocky artefacts which look particularly unpleasant. JPEG images look particularly bad around the sharp edges of objects.

There are already ways to reduce the artefacts, however, these methods often don’t use very sophisticated techniques, only using the information from adjacent pixels to smooth out the actual transition between the blocks. An example of this can be found in Kitbi and Dawood’s work https://ieeexplore.ieee.org/document/4743789/ which gave me the original inspiration for this.

An alternative way is to use a convolutional neural network (CNN) to intelligently estimate an optimal block given the original block and the eight surrounding blocks. And then tile over the image to estimate the optimal mapping for each block.

The network design was a 5 layer fully convolutional one, using only small filters. Several different architectures were used, which all gave largely similar results. The compromise between effectiveness and speed (i.e. 1/size) was found with a small network with only 57,987 parameters. Training the network was surprisingly fast, taking only a few hours without a GPU.

The network takes in full colour information and outputs the full colour too. The reason for this is to use all of the possible information. The colour channels are highly correlated with one another. It would be possible to train the network on monochrome images, but that would lose the relation which naturally exists.

So, does it work?

In my opinion, yes it does work. I think my method performs best when there are complicated edges, such as around glasses, or on hairs which are resolved as partial blocks. It works least well, in comparison to the method which photoshop currently uses, when there are large smooth areas.

Text was not present in the training data set. So the poor effectiveness of the network on text is not a significant point of comparison. The above images are quite small. A larger example is below, along with a zoomed in video comparing the original, JPEG, photoshop artefact removal, and my method.

I did calculate root mean squared error values one point comparing the network performance with the JPEG image to the original. In some cases the network was reliably out performing the JPEG – which is impressive, but not too surprising, as this was how it was trained. I don’t think that those sorts of values are too important in this case. The aim isn’t to restore the original image, but to instead reduce the visual annoyance of the artefacts.

If you really wanted to reduce the annoyance of the artefacts you should use JPEG2000 or else have a read of this paper https://arxiv.org/pdf/1611.01704.pdf

Linify: photographs to CNC etch-a-sketch paths

Projects

Linify: def. to turn something into a line.

I saw someone the other day using a variable density Hilbert curve to transform an image so as to be projectable using a laser and galvo mirror setup, this was on the facebook page Aesthetic Function Graphposting.

That kinda stayed in the back of my mind until I saw This Old Tony’s youtube video about making a (computer numeric controlled) CNC etch-a-sketch. The hardware looked great, but he was just using lame line sketches of outlines, the kind of limited images which you’d expect from an etch-a-sketch.

So, I put together a lazy easy way of turning a photo into a single line. Here is an example of my face. If you move quite far back from the image, it looks pretty good.

It uses a variable amplitude sinewave patches, which have a whole number of periods. Sine waves are used due to their simplicity and their periodicity. The same effect could be achieved with other periodic waves, in fact, square waves may be more efficient for CNC applications, as fewer commands would need to be issued to the orthogonal control axes.

The image is first downsampled to a resolution around 64 px on an edge. Then, for each pixel in the downsampled image, an approximate sinewave is found. Blocks of sine waves are added to a chain, which runs over the whole image. Currently, it raster scans, but it would be pretty easy to go R->L on even and L->R on odd. To improve the contrast, the downscaled image is contrast stretched to the 0-1 interval, and then each intensity value is raised to the (default) power of 1.5, this gives a little more contrast in the lighter regions and compensates somewhat for the low background level and the non-linear darkening with greater amplitude. This could be tuned better.

There are several factors which alter the contrast. The cell size, frequency, number of rendered points, linewidth, and also the gamma-like factor applied to the image before the linify. Images were then optimised by adjusting the gamma-like factor. Optimal values were found between ~0.75 and ~1.65. Higher values were better for darker images. Successive parabolic interpolation (SPI) was used, four values were selected at random, and their error with respect to the original image was found. These values were then used to fit a parabola, and the minima of the parabola were used as a new point. This process was iterated with the four best values being used for the fit. This process can be seen in the figures below. In the first figure, four points (the blue stars) are found. The first parabola is fitted, and the red point is the predicted best parameter value. In the second figure, the blue star shows the true value of the metric we are trying to minimise, it is slightly different than predicted. A new estimated best parameter value (green) is found. And so on. To ensure that the parabola is only used near the minima of the function, the points farthest from the minima are discarded. Typically, only three points are used, my implementation uses four for robustness, which is helpful as the curve is non-analytic and non-smooth.

A few starting locations were checked to ensure that the minimum found was global. This kind of root finding, SPI, is very simple and commonly used. It converges faster than a basic line search (about 33% faster) but does not always converge to the local extremum. Parabola are used, as the region around any minima or maxima of any function can be approximated by a parabola, which can be observed by the Taylor expansion about an extremum.

Whilst we have a non-linear intensity response and some artefacts from the process, it is much easier to get this kind of process to well represent real images than the skittliser process, as we have a wide range of possible intensity levels.

Of course, one of the issues with using this method on something like an etch-a-sketch is the extremely long paths taken without any kind of reference positions. Modifications could be made internally to an etch-a-sketch to have homing buttons which would click at certain x or y positions, thus giving the control system a method of resetting itself at least after every line. A much more difficult, but potentially interesting closed-loop control system would be using information from a video feed pointed at the etch-a-sketch. Taking the difference of successive frames would likely be a good indication of the tip location.

Finally, here is a landscape photograph of a body of water at sunrise. Just imagine it in dusky pink.

Skittleiser

Projects

In this short project, which I finished in December of 2017, I took colour photos and represented them using images of skittles. To start off, I found photographs of skittles on the internet and segmented out the skittles manually. I was going to use my own images, but there are some flavours of skittles, which I couldn’t find at the time, and I wanted to get started right away. Since then, I have produced a library of my own skittle photos.

There were I found eight skittle colours in total: blue, green, orange, pink, purple, white, yellow, and red. The purple skittles are very dark and look like black in contrast to the other colours. In a short python programme, I extracted small chips of an input photo and compared it to the images of the skittles. The programme then rotated the skittle image through 90, 180, and 270 degrees to see which was were best fit for the photo chip. These skittle images were then saved.

I quickly swapped to using my own skittle images, where possible. On a sheet of white paper and with a flash I took some photos of the contents of a small packet of skittles. For some reason, after each shot, the number of remaining skittles decreased. In another short python script, I used the open computer vision library to segment out the skittles and save them. I used a few steps to do this. I collapsed the images to greyscale and then blurred it and thresholded the image to produce a black and white image. This created white and black regions which corresponded to the location of the skittles, but also found regions in the background made up of noise. I then used two morphological operations, an erosion followed by a dilation. Erosion makes make black regions smaller by a set amount, and dilation makes those regions larger again. This is very useful for removing small regions in image processing tasks, like noise. Noise regions are often small enough to be removed completely when eroded, and the larger skittles are only reduced in size. I then found the location of the edges of the black regions and used this to cut out the skittles.

So, how delicious would portraits made out of skittles be? Well, I don’t know, as I never made any out of actual skittles. To get a decent, recognisable image you need about 10 kS (that’s kiloSkittles), or around 100 skittles on the short edge. Since skittles are about 1cm wide, it would be quite a large structure. On top of that, skittles also weigh about a gram, which would mean you’d need ~10kg of skittles, and at a penny a sweet you’d spend £100. That assumes that you can bulk buy the correct colours, which isn’t the case, most of the images I produced are mostly purple or yellow, with very little green.

Bulk buying individual colours would make it feasible, but still not trivial. And then there’s the placing of >10 kS, although I can see that being quite therapeutic. I assumed that setting them in resin would be sufficient to preserve them, their high sugar content and a lack of oxygen should probably stop them from changing much over months, but I don’t know what might happen over a period of years.

If I ever revisit the idea I’ll add a hexagonal stacking mode, as well as the option to include dithering for greater colour accuracy. I have already added functionality for rectangular images of skittles from the side, to increase the resolution of the image in one direction. This worked, but the results weren’t as pleasing. I imagine, with the skittles on their sides, it would be that much harder to assemble.

Dithering is an interesting concept. This medium renders images in an unusual way. If we forget about photons, the intensity of light on a given area is a continuous property, it could be twice as much as another area, or half as much, or any fraction. Digital cameras quantise this level when the analogue signal (a voltage) is converted to a digital level in a range. On dSLRs this is range is typically 12-14 bits or between 4096 and 16,384 levels. This is often then down-converted to 8 bits (256 levels) if the image is saved as a jpg, but the full range is sometimes kept with other file types.

256 intensity levels for each colour channel is sufficient for viewing or printing images. The ability of the eye to differentiate between intensity levels is dependent on a large number of factors, including the absolute intensity of the source, as well as the colour. Colour photos allow the representation of a large number of colours and shades, typically 16.8 million. These colours can be represented in Hue, Saturation, Value or HSV space. HSV breaks down a pixel into its ‘value’, the brightness of the pixel, ‘hue’ the pure colour of the pixel, and ‘saturation’ which is how vivid the colour is, or how much of the pure colour is mixed with white. Now, our skittles well sample the different hues which are in photos, but they do not well sample any of the other dimensions of HSV space. Purple skittles are the only dark skittles, and the rest of them are all highly saturated bright colours, save for white, which is still bright. Because of this, many images cannot be well represented by skittles (I know, who’d have thought that?).

This is where dithering comes in. Dithering, in this case, trades of spatial resolution for better colour representation. A small image patch is considered, and the average colour in that patch is matched to several skittles. A light pink area, without dithering, would be represented as (say) four white skittles. But with dithering, one or two of the skittles could be swapped to red or pink. When viewed from a distance this would look much like a lighter pink. This would allow for areas of tone which are all similar to skittle colours to show some detail, and also allow for more accurate representation of the colour of image regions which are not well represented by skittle colours.

Dithering does have some disadvantages. You lose spatial resolution, as boundaries between colours are blurred to intermediate values. It also doesn’t make ‘sense’ when viewed close up. A flat light pink region of an image may have a bright red skittle in the middle of it, and it might not be obvious from the original image why it is there.

I quite like them, anyway.

Joshua McBruceer

Photography and Projects

Computational photography

Zeiss Tessar: How does my vintage lens blur images?

JPEG artifact removal with Convolutional Neural Network (AI)

Linify: photographs to CNC etch-a-sketch paths

Skittleiser